キーワード: 逆散乱理論、ウエーブレット解、高次元デ―タ解析、トモグラフィー、幾何解析
http://fc.jpn.org/inverse-problem/

インタビュイー:磯崎 洋 教授(前代表)
数学・物理学で古くから知られる逆問題の計算手法は、数学者と他分野の研究者との異分野融合研究の中で様々な応用が試みられ始めました。この手法で様々な対象の内部構造の探査にチャレンジしてゆきます。
順問題と逆問題

図1:体の断面に見立てた数理モデル。内臓(紺)と腫瘍(赤)を含む。右:逆問題の手法で推測
数学や物理学には順問題と逆問題というものがあります。ある音源から音を発すとき、幾つかの物体に反射されて戻って来る音の大きさを計算するのが順問題であり、配置の情報から反射音の情報が導かれます。その逆に反射音の情報から物体の配置情報を推定するのが逆問題であり、この手法は魚群の探知や内臓の検査に現在広く用いられています。一般に、逆問題では「音」のような単純な(低い次元の)情報から内臓画像のような複雑な(高い次元の)情報を推定することが要求されるところに原理的な難しさがあります。数学はその困難を、1) 複数の仕方で観測された単純情報を組み合わせて情報を増やす、2) 低次元情報と高次元情報の密接な結びつきが理論的にわかっている特別なケース(解析性など)を当てはめる、といった手法で乗り越えます。後者の代表例は「境界値逆問題」です。図1左のような人体のモデルを考えるとき内臓や腫瘍で電流の流れ方が異なりますが、体の表面の電流の様子を調べるだけで体内の電流を推測し、結果的に内臓や腫瘍の位置を推定できます(図1右)。フィンランドの研究仲間とともに、これを本物の人体に応用する計画が進んでいます(図2)。

図2:ヘルシンキ大学Samuli Siltanen 教授が自ら体表の電流測定テスト
応用範囲は多様
他のさまざまな物質の内部構造の推定にも逆問題の手法は使われ始めています。例えば炭素の同位体が6角格子と呼ばれる構造で構成されている“グラフェン”の内部構造の推定(図3)。また、老朽化した鉄橋の金属内部の欠陥を見つけるための応用も考えられています。欠陥のある場所では局所的に温度が変化することを利用する技術です。このように逆問題の手法は数学と他分野の融合研究の好例となっています。
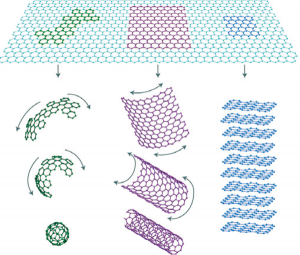
図3:グラフェンの構造、以下より抜粋
“PROPOSAL for the ‘Strategic Innovation Agenda’ (SIA) for the EIT written by Prof. Lászlo P. Biró Nanostructures Dept. Research Institute for Technical Physics and Materials Science, Budapest, Hungary”
社会への貢献・実績
● アメリカの学術専門雑誌“Inverse Problems and Imaging”編集委員
取材:平成27年8月17日
Non-Destructive Inspection by the Technique of Inverse Problem
Unit name: Research unit for inverse problems
Key words: inverse scattering theory, wavelet solution, high-dimensional data analysis, tomography, geometric analysis

interviewee; Isozaki, Hiroshi
The calculation technique for “inverse problem,” known since many years ago in the fields of mathematics and physics, has recently begun to be applied in various ways to multidisciplinary fused research by mathematicians and researchers in other fields. We will make a challenge of exploring the inner structure of various objects with the use of this technique.
Forward Problem and Inverse Problem

Fig. 1: A mathematical model of human body cross-section. Internal organs (blue) and tumor (red) are included in the model. Right: Estimation with the technique of inverse problem.
In mathematics and physics, forward problems and inverse problems are encountered. An example of forward problem is calculation of the intensity of the sound returning by reflection on several materials after being generated from a sound source. In this case, the information on the reflective sound is derived from the information on arrangement/distribution. A reversed procedure, i.e. estimation of the information on material arrangement/distribution from the information on reflective sound, is an inverse problem. This technique is now used extensively for fish finders and clinical checks of internal organs. Inverse problems generally involve a difficulty related to principle, because complicated information (information of higher dimensions) needs to be estimated from simple information (information of lower dimensions) such as “sound.” Mathematics attempts to overcome such difficulty by using the following techniques: (1) increasing the available simple information by means of combining the pieces of such information in a complicated manner, and (2) applying a special case (with specific analytical potential, etc.) known theoretically to have connection of low-dimensional information to high-dimensional information. A representative example of the latter case (2) is “inverse boundary value problem.” In a human body model shown in Fig. 1 (left), the way of electricity flow differs among organs or tumors, but the electric current within the living body can be estimated simply from investigation of the superficial electrical current of the living body, resulting in estimation of the location of internal organs or tumors (Fig. 1, right). A project to apply this technique to real human bodies is now under way jointly with Finnish researchers (Fig. 2).

Fig. 2: Electric current measurement on his own body surface by Prof. Samuli Siltanen (University of Helsinki)
Wide Scope of Application
The technique of inverse problem has begun to be used also for estimation of the inner structure of other various materials. For example, it is used for estimation of the inner structure of “graphene” composed of carbon isotopes forming a hexagonal grid structure (Fig. 3). Its application to detection of defects inside the metals constituting old iron bridges has also been considered. This technology utilizes the fact that local changes of temperature are seen at the defective sites. Thus, the technique of inverse problem has become a good example of the topics for research combining mathematics with other academic fields.

Fig. 3: Structure of graphene (excerpts from the following paper)
Social contributions and achievements
Editorial Board member of the American professional journal “Inverse Problems and Imaging”
Interviewed on August 17, 2015
